RNA biophysics
My interest in the physics of RNA originated in my work on the physics of RNA viruses, where we have
shown that the physical compactness of viral RNA genomes is a property encoded in their genomic sequence—as an additional layer of information to that of protein-coding regions. The (yet unanswered) question to how RNA sequence can encode for its physical properties has led me to
start exploring in detail the connections between RNA sequence, structure, and its functions. Since
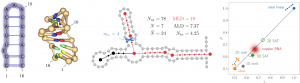
the highly branching nature of RNA structure is a likely candidate for some of its physical properties,
including size and functionality, we have started to develop the description of RNA as a (randomly) branching polymer. Using it, my coworkers and I have been the first to derive the topological scaling
exponents of RNA in this framework and connect them with physical properties. We have also shown how the scaling exponents can be derived from individual RNA sequences—important for biological systems—and have started to apply this approach to the genomes of RNA viruses.
Selected publications:
- D. Vaupotič, J. Morand, L. Tubiana, and A. Božič, “Designing the phase space of topological indices of branched macromolecules,” arXiv:2409.16007 [cond-mat.soft].
- V. Bukina and A. Božič, “Context-dependent structure formation of hairpin motifs in bacteriophage MS2 genomic RNA,” Biophys. J. 123 (2024) 3397–3407.
- D. Vaupotič, A. Rosa, L. Tubiana, and A. Božič, “Scaling properties of RNA as a randomly branching polymer,” J. Chem. Phys. 158 (2023) 234901.
|
Physical virology
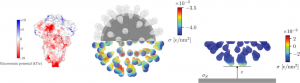
I have worked extensively on various aspects of the physics of (mostly RNA) viruses. Apart from looking into the properties of their genomes, my coworkers and I have also been exploring how charge-induced changes in the ordering of their capsid proteins leads to conformational changes in
the capsids during their maturation. I have also invested significant effort into applying our knowledge to the study of the SARS-CoV-2 virus and its properties during the COVID-19 pandemic. With my coworkers we have, for instance, shown how the virus interacts with a charged electret fibre—as found in face masks—due to the charge on its spike protein. I have also made a series of studies elucidating evolutionary changes in the charge on the spike protein as the pandemic has progressed, uncovering a clear tendency towards an increase in the amount of positive charge on the spike protein. Furthermore, I have co-written a well-received review aimed at non-specialists on the role of relative humidity in the spread of airborne diseases, with a particular focus on respiratory viruses.
Selected publications:
- A. Božič and R. Podgornik, “Changes in total charge on spike protein of SARS-CoV-2 in emerging lineages,” Bioinform. Adv. 4 (2024) vbae053.
- S. Rochal, D. Roshal, A. Božič, I. Golushko, and R. Podgornik, “Packing and
trimer-to-dimer protein reconstruction in icosahedral viral shells with a single type of
symmetrical structural units,” Nanoscale Adv. 4 (2022) 4677–4688.
- A. Božič and M. Kanduč, “Relative humidity in droplet and airborne transmission of disease,” J. Biol. Phys. 47 (2021) 1–29.
|
Electrostatics in colloidal and protein systems
My work on various aspects of electrostatics in soft matter and biological systems has recently led me
to start developing the theory of the mechanism of charge regulation—by which biological molecules
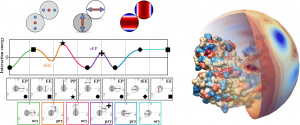
acquire charge—in globular proteins and patchy colloids. Besides developing theoretical frameworks
for the study of charge regulation in spherical particles, I have recently worked on generalising the
Kirkwood-Shumaker theory of protonation fluctuations to inhomogeneously charged globular proteins.
Selected publications:
- A. Gnidovec, E. Locatelli, S. Čopar, A. Božič, and E. Bianchi, “Anisotropic DLVO-like interaction for charge patchiness in colloids and proteins,” arXiv:2411.03045 [cond-mat.soft].
- A. Božič and R. Podgornik, “Anomalous multipole expansion: Charge regulation of patchy, inhomogeneously charged particles,” J. Chem. Phys. 149 (2018) 163307.
- A. Božič and R. Podgornik, “pH dependence of charge multipole moments in proteins,” Biophys. J. 113 (2017) 1454–1465.
|
Classification of order on spherical surfaces
A large part of my work has dealt with systems with spherical geometry—from viruses and globular
proteins to pollen grains, patchy colloids, and assemblies of particles on the sphere. This has naturally
led me to consider the classification of order in such systems, and in 2019, we have managed to rigorously extend the concept of hyperuniformity—a type of order which has up to that point been explored only in Euclidean space—to spherical geometry. We have later extended this notion to particle systems best described by vector and tensor spherical harmonics (i.e., particles with dipolar or quadrupolar symmetry). In the scope of this, we were also the first to develop an algorithm for the measure of overlap between spherical ellipses.
Selected publications:
- A. Gnidovec, A. Božič, and S. Čopar, “Dense packings of hard ellipses on a sphere,” Soft Matter 18 (2022) 7670–7678.
- A. Gnidovec, A. Božič, U. Jelerčič, and S. Čopar, “Measure of overlap between two arbitrary ellipses on a sphere,” Proc. Roy. Soc. A 478 (2022) 20210807.
- A. Božič and S. Čopar, “Hyperuniform particle distributions on the sphere,” Phys. Rev. E 99 (2019) 032601.
|